给你一个整数 n 表示某所大学里课程的数目,编号为 1 到 n ,数组 dependencies 中, dependencies[i] = [xi, yi] 表示一个先修课的关系,也就是课程 xi 必须在课程 yi 之前上。同时你还有一个整数 k 。
在一个学期中,你 最多 可以同时上 k 门课,前提是这些课的先修课在之前的学期里已经上过了。
请你返回上完所有课最少需要多少个学期。题目保证一定存在一种上完所有课的方式。
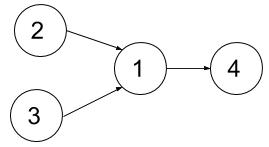
输入:n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2 输出:3 解释:上图展示了题目输入的图。在第一个学期中,我们可以上课程 2 和课程 3 。然后第二个学期上课程 1 ,第三个学期上课程 4 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/parallel-courses-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
class Solution {
int[] mask=new int[15];
int[] dp=new int[1<<15];
int[] cnt=new int[1<<15];
//dp[state] 表示上完状态为state的课程需要多少学期 state第n位为1 则说明课程n已经上过了
//state第n位为0 则说明课程n还没上过
//mask[i] 表示课程i需要先修课程的掩码 mask[i]第j位为1说明 第j门课是i的先修课程 为0 则说明第j门课不是i的先修课程
//cnt[state] 表示状态state中1的个数 也就是state下已完成课程的数目
public int minNumberOfSemesters(int n, int[][] dependencies, int k) {
int N=1<<n;
for(int i=0;i<n;i++) mask[i]=0;
//只需记录上一级的先修课程 先修课程的先修课程不需要记录
//因为只有先修课程的先修课程上完 先修课程才能上
for(int[] d:dependencies) mask[d[1]-1] |=1<<(d[0]-1);
cnt[0]=0;
for(int i=1;i<N;i++) cnt[i]=cnt[i>>1]+(i&1);
for(int i=1;i<N;i++) dp[i]=16; //天数最多为15
dp[0]=0;
for(int i=0;i<N;i++)
{
if(dp[i]<=n) //上完所有课最多需要n学期 如果dp[i]>n 说明i状态无法达到
{
//System.out.print(i+" ");
// i为所有课程的完成状态 j为课程序号
//(i>>j& 0x1)==0 表示i的第j位不是1说明 该课程还没有上
//(mask[j] & i) == mask[j] 说明课程j的先修课程已经上完(i中对应mask[j]所有为1的bit也为1)
//上述条件满足的情况下 将cur的第j位置1 说明该课程可以在当前学期完成
int cur=0;
for(int j=0;j<n;j++)
{
if( (i>>j& 0x1)==0 && (mask[j] & i) == mask[j] ) cur|=1<<j;
}
//l中包括了当前学期内所有可以完成的课程 其中的课程可以选择在本学期完成 也可以不在
// j-1 & l 表示逐步将l中的1从低位开始 每次迭代减少一个(课程)
//当前状态j中的课程数o[j]小于k 说明可以在本学期完成 因此将j中课程加入原始状态i( i|j )
//dp[i]+1 表示学习天数增加一天
for(int j=cur;j!=0;j=j-1&cur)
{
if(cnt[j]<=k) dp[i|j]=Math.min(dp[i|j],dp[i]+1);
}
}
}
return dp[N-1];
}
}